Главная | Обратная связь

Означення логарифма.

 

Логарифмом числа b за основою а називають показник степеня, до якого треба піднести а, щоб дістати b.

Записують це так log_a b.

Приклад.

Вираз log_a b має зміст, якщо а > 0, а ≠ 1 і b > 0.

2. Десятковий і натуральний логарифми.

 

Логарифм числа b за основою 10 називають десятковим і позначають lg b.

Приклад.

Якщо основою логарифма є число е (е ≈ 2,718281... ), то логарифм числа b за основою е називають натуральним і позначають ln b.

3. Властивості логарифмів.

 

Основна логарифмічна тотожність
loga 1 = 0
Логарифм добутку
Сума логарифмів
Логарифм частки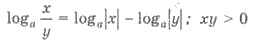
Різниця логарифмів
Логарифм степеня
Формули переходу до іншої основи

 

Розглянемо приклади використання властивостей логарифмів при обчисленні виразів.

Приклад 1.

 

Приклад 2. Прологарифмувати вираз за основою 2.

Розв’язання.

Тотожні перетворення, що містять логарифми.

 

Приклад 1. Знайти х, якщо

Розв’язання. Спочатку перетворимо праву частину

Отже, 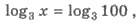а тому х = 100.

Приклад 2. Дано Виразити через m і n:

Розв’язання.

Приклад 3. 1) Довести формулу:

2) Порівняти

Розв’язання. що й треба було довести.

2) Оскільки

Приклад 4. Обчислити: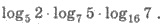

Розв’язання. Перейдемо до основи 2:

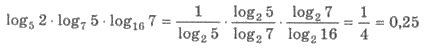
Приклад 5. Обчислити:

Розв’язання.

Приклад 6. Дано Знайти значення виразу

Розв’язання. Оскільки Крім того а тому Маємо

Приклад 7. Порівняти log₁₃₅ 675 і log₄₅ 75.

Розв’язання.

Позначимо log₃ 5 = а > 1. Розглянемо різницю:

Отже,

КОНТРОЛЬНИЙ ТЕСТ № 9

 

1. Яка з рівностей правильна?

 

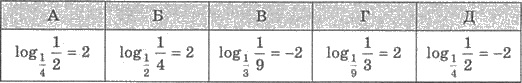
2. Який з виразів не має змісту при х = 2?

 

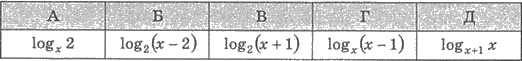
3. Знайти значення виразу:

 

4. Обчислити:

 

5. Знайти значення виразу:

 

6. Дано числа Розмістити ці числа у порядку спадання.

 

7. Обчислити:

 

8. Між якими двома сусідніми цілими числами знаходиться значення виразу

 

9. Обчислити: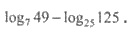

 

10. Дано: Виразити через а і b значення виразу log₂ 45 .

 

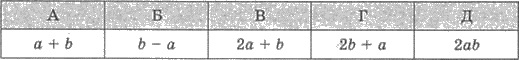
11. Знайти значення виразу:

 

12. Знайти х, якщо