Главная | Обратная связь

Знаки тригонометричних функцій по чвертях.

 

Синус кута а є ординатою точки Р_α(х;у) одиничного кола (мал. 19). У І та II чвертях у > 0, а у III та IV чвертях у < 0. Тому sin α > 0, якщо α — кут І або II чверті, і sin α < 0, якщо α — кут III або IV чверті.

Косинус кута α є абсцисою точки Р_α(х;у) одиничного кола (мал. 19). У І та IV чвертях х > 0, а у II та III чвертях х < 0. Тому cos α > 0, якщо α — кут І або IV чверті, і cos α < 0, якщо α — кут II або III чверті.

Оскільки то tgα і ctg α залежать від знаків sin α і cos α. У І та III чвертях sin α і cos α мають однакові знаки, а у II та IV чвертях різні. Тому tg α > 0 іctg α > 0, якщо α — кут І або III чверті, і tg α < 0 і ctg α < 0, якщо α — кут II або IV чверті.

Знаки тригонометричних функцій у кожній з чвертей подано на малюнку 21.

 

 

Приклад. Порівняти з нулем: 1) соs152°; 2) tg3 ∙ sіn4 .

Розв’язання. 1) Оскільки 152° — кут II чверті, то соs152° < 0 .

2) 3 радіани ≈ 3 ∙ 57° = 171°, тому 3 радіани — кут II чверті і tg3 < 0 .

4 радіани ≈ 4 ∙ 57° = 228°, тому 4 радіани — кут III чверті і sіn4 < 0. Остаточно маємо tg3 ∙ sіn4 > 0 .

4. Парність і непарність тригонометричних функцій.

 

Косинус — функція парна; синус, тангенс і котангенс — непарні:

Приклади.

Періодичність тригонометричних функцій.

 

Періодом функцій косинус і синус є 360° (2π радіан), а функції тангенс і котангенс — 180° (π радіан).

У вигляді формул це можна записати наступним чином:

 

для кута α у градусах
для кута α у радіанах

 

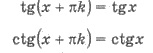
Зважимо, що в усіх формулах k — ціле число, а у формулах для тангенса і котангенса розглядаються лише допустимі значення α і х.

Приклади.

СПІВВІДНОШЕННЯ МІЖ ТРИГОНОМЕТРИЧНИМИ ФУНКЦІЯМИ ОДНОГО Й ТОГО САМОГО АРГУМЕНТУ.

Тотожності, що пов’язують тригонометричні функції одного й того самого аргументу.

 

Використання співвідношень між тригонометричними функціями одного й того самого аргументу для обчислень.

 

Приклад 1. Знайти sin α , якщо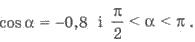

Розв’язання. Оскільки α — кут II чверті, то sin α> 0. Маємо

Приклад 2. Знайти tg x, sinх, cos х, якщо

Розв’язання.

Оскільки х — кут IV чверті, то sіnx < 0, тому