Главная | Обратная связь

ТОТОЖНІ ПЕРЕТВОРЕННЯ РАЦІОНАЛЬНИХ ВИРАЗІВ

 

Приклад 1. Довести тотожність:

Доведення.

що й треба було довести.

Приклад 2. Спростити вираз:

Розв’язання.

Відповідь. .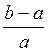

Приклад 3. Обчислити значення виразу:

Розв’язання. Спростимо вираз:

3) Якщо х = 2,01, то маємо

Відповідь. 401

СТЕПІНЬ З ЦІЛИМ ПОКАЗНИКОМ.

Означення степеня з цілим показником.

 

Якщо a ≠ 0 і n - натуральне число, то

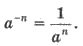
Приклади.

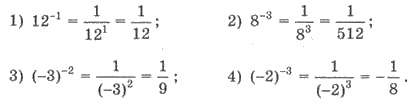
Корисною є формула

Приклади.

Властивості степеня з цілим показником

 

Властивості степеня з цілим показником такі самі, як і властивості степеня з натуральним показником (див. §9, п. 2).

Розглянемо застосування цих властивостей.

Приклад 1. Знайти значення виразу:

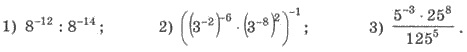
Розв’язання.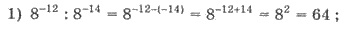

Приклад 2. Спростити вираз:

Розв’язання.

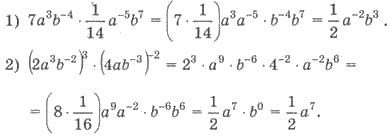
КОНТРОЛЬНИЙ ТЕСТ № 4.

 

1. При якому значенні вираз не має числового значення?

2. Спростити дріб: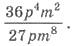

 

3. Звести дріб 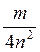до знаменника 20n²m.

4. Спростити вираз:

5. Виконати додавання дробів: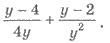

6. Виконати множення дробів: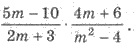

7. Піднести до степеня:

8. Виконати ділення:

9. Обчислити: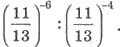

10. Спростити вираз:

11. Знайти значення виразу у = 2012.

 

12. Обчислити: 1,25^-2 + 2,5^-3.

КВАДРАТНІ КОРЕНІ. АРИФМЕТИЧНИЙ КВАДРАТНИЙ КОРІНЬ.

Означення квадратного кореня.

 

Квадратним коренем з числа а називають число, квадрат якого дорівнює а.

Квадратним коренем з числа 16 є числа 4 і -4 (бо 4² = 16 і (-4)² = 16).

2. Означення арифметичного квадратного кореня.

Арифметичним квадратним коренем з числа а називають таке невід’ємне число, квадрат якого дорівнює а (позначають ).

Наприклад:

Властивості арифметичного квадратного кореня.

 

 

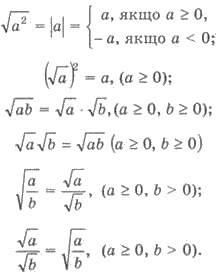
Розглянемо приклади застосування цих властивостей.

Приклади.

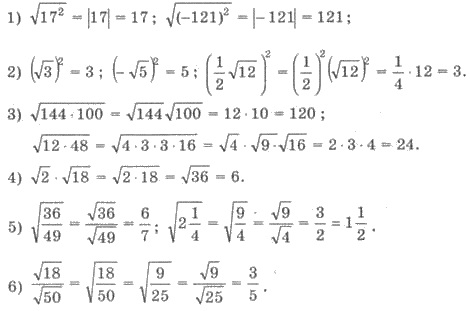
Дії з арифметичними квадратичними коренями.

 

Розглянемо приклади дій з арифметичними квадратними коренями.

Приклади.

ТОТОЖНІ ПЕРЕТВОРЕННЯ ВИРАЗІВ, ЩО МІСТЯТЬ КВАДРАТНІ КОРЕНІ.