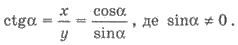Главная | Обратная связь

Кут довільної величини.

 

Розглянемо одиничне коло. Радіус ОА, де А(1;0) назвемо початковим радіусом (мал. 10).

 

 

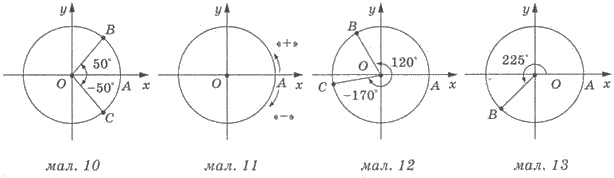
Повернемо радіус ОА навколо точки О на 50° проти руху годинникової стрілки. Тоді радіус ОА займе положення ОВ. Кажуть, що кут повороту дорівнює 50°. Повернемо тепер початковий радіус ОА на кут 50° за рухом годинникової стрілки; отримаємо радіус ОС. В цьому випадку кажуть, що кут повороту дорівнює -50°. На малюнку 10 стрілками показано кути повороту 50° і -50°. Взагалі, при повороті початкового радіусу проти годинникової стрілки, кут повороту вважається додатнім, а за рухом годинникової стрілки — від’ємним (мал. 11).

Кут повороту може бути будь-яким дійсним числом. На малюнку 12 показано кути повороту 120° і 170°.

Щоб позначити кут повороту 225°, спочатку повернемо початковий радіус ОА на 180° проти руху годинникової стрілки, а потім ще на 45° в тому самому напрямі (180° + 45° ==225°). На малюнку 13 стрілкою показано кут повороту 225°.

 

 

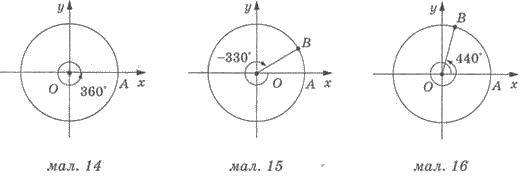
Якщо початковий радіус зробить повний оберт проти руху годинникової стрілки, то кут повороту дорівнюватиме 360° (мал. 14).

На малюнку 15 показано кут повороту -330°, а на малюнку 16 — кут повороту 440°.

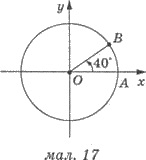
Нехай при повороті на кут 40° початковий радіус ОА перейшов у радіус ОВ (мал. 17). Якщо після цього радіус ОВ повернути на кут 360° або -360°, то знову отримаємо радіус ОВ. Таким чином зробимо висновок про те, що радіус ОА переходить в радіус ОВ й при повороті на кути 40° + 360° = 400° і 40° - 360° = -320° та й узагалі при повороті на кут40° + +360°k, де k — будь-яке ціле число (k 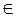Z).

 

 

З іншого боку, будь-який кут а можна подати у вигляді α = α₀ + 360°k, де 0 ≤ α₀ < 360°, k — ціле число.

Наприклад: 1100° = 20° + 360° ∙ 3 ; - 640° = 80° + 360° ∙ (-2).

З геометрії відомо, що координатні осі поділяють координатну площину на чотири чверті (мал. 18). Якщо при повороті на кут а початковий радіус ОА перейшов у радіус ОВ, то залежно від того, в якій координатній чверті буде цей радіус, кут а називають кутом цієї чверті.

 

 

Приклад. Кутом якої чверті є кут:

1) α = 1999°; 2) β = -2010°.

Розв’язання. 1) Оскільки α = 1999° = 199° + 360° ∙ 5, то α = 1999° — кут III чверті.

2) Оскільки (3 = -2010° = 150° + 360°(- -б), то р = -2010° — кут II чверті.

4. Тригонометричні функції кута і числового аргументу.

 

Нехай при повороті на кут а початковий радіус ОР₀ одиничного кола переходить у радіус ОР_α , де Р_α має координати (х;у) (мал. 19).

 

 

Кажуть що куту а відповідає точка Р_α одиничного кола. Тоді:

1) синусом кута α називають ординату точки Р_α(х;у) одиничного кола: sіn α = у ;

2) косинусом кута α називають абсцису точки Р_α(х;у) одиничного кола: соs α = х ;

3) тангенсом кута α називають відношення ординати точки Р_α(х;у) одиничного кола до її абсциси: tg α = y/x (якщо х ≠ 0 );

4) котангенсом кута α називають відношення абсциси точки Р_α(х;у) одиничного кола до її ординати: ctg α = x/y (якщо у ≠ 0).

Зауважимо, що α може вимірюватися як у градусах, так і в радіанах.

Дане вище означення тангенса можна замінити рівносильним йому означенням: тангенсом кута α називають відношення синуса цього кута до його косинуса.

Дійсно,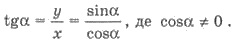

Аналогічно:

котангенсом кута α називають відношення косинуса цього кута до його синуса.