Главная | Обратная связь

Означення алгебраїчного дробу.

 

Раціональний вираз вигляду a/b, де а і b - вирази, що містять числа або змінні, називають дробом, де а - чисельник цього дробу, b - його знаменник.

Якщо чисельник і знаменник дробу - многочлени, то дріб називають алгебраїчним дробом або раціональним дробом.

Приклади алгебраїчних дробів: тощо.

Область допустимих значень змінних.

 

Значення змінних, при яких вираз має зміст, називають допустимими значеннями змінних. Ці значення утворюють область допустимих значень змінних (або область визначення).

Приклад. Знайдіть допустимі значення змінних у виразах:

Розв’язання. 1) Вираз має зміст при будь-яких значеннях змінної а.

2) Допустимі значення змінної у - усі числа, крім числа -3, оскільки якщо y = -3, то знаменник дробу перетворюється на нуль.

3) Знаменник дробу перетворюється на нуль, якщо х = 0 або х = 3.

Тому допустимі значення змінної х - усі числа, крім 0 і 3.

Основна властивість дробу.

 

Якщо чисельник і знаменник дробу помножити або поділити на один і той самий вираз, то дістанемо дріб, який дорівнює даному.

Скорочення дробу.

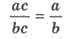
Приклади:

Зведення дробу до нового знаменника.

 

Приклад. Звести дріб:

1) до знаменника 15х²; 2) до знаменника а³ – b³.

§15. ПРАВИЛА ВИКОНАННЯ АРИФМЕТИЧНИХ ДІЙ З АЛГЕБРАЇЧНИМИ ДРОБАМИ.

Додавання і віднімання дробів з однаковими знаменниками.

Приклади.

 

Розв’язання.

Додавання і віднімання дробів з різними знаменниками.

 

Додавання і віднімання дробів з різними знаменниками доцільно виконувати за наступним планом:

1) розкласти на множники знаменники дробів, якщо це необхідно;

2) визначити спільний знаменник, бажано найпростіший;

3) записати додаткові множники;

4) знайти дріб, що є сумою або різницею дробів;

5) спростити цей дріб та дістати відповідь.

Приклади.

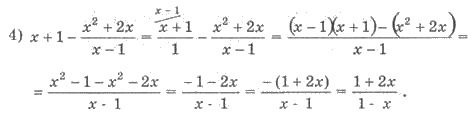
Множення дробів

 

Приклади.

Піднесення дробу до степеня

 

Приклади.

Ділення дробів

 

Приклади.