 |
|
Означення, зображення та позначення числового проміжку.
Позначимо на координатній прямій точки із координатами 1 і 4 (мал. 3). Якщо точка розташована між ними, то їй відповідає число, яке більше 1, але менше 4. Вірне і обернене: якщо число х задовольняє умову 1 < x < 4 , то воно зображується точкою, що лежить між точками з координатами 1 і 4. Множину всіх чисел, що задовольняють умову 1 < х < 4 , позначають числовим проміжком від 1 до 4. позначають його так (1; 4). Цей проміжок зображено на малюнку 4.
bbsp;
На малюнку 5 зображено множину точок, що задовольняє умову 2 ≤ х ≤ 7 . Позначають його так [2; 7].
Дано таблицю, в якій відображено відповідність між умовою, зображенням на малюнку та позначенням.
| № | Умова | Зображення на малюнку | Позначення |
| х < а |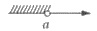 
| (-∞ ; а) | |
| х ≤ а | 
| (-∞ ; а] | |
| х > а |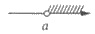 
| (а; +∞) | |
| х ≥ а | 
| [а;+∞) | |
| а < х < b | 
| (а; b) | |
| а ≤ х < b | 
| [а; b) | |
| а < х ≤ b | 
| (а; b] | |
| а ≤ х ≤ b | 
| [а; b] |
2. Переріз та об’єднання числових проміжків.
Перерізом числових проміжків називають множину, що складається з чисел, які належать кожному з цих проміжків.
Знак ∩- знак перерізу.
Наприклад, 
(ілюстрація на малюнку 6), а 
(ілюстрація на малюнку 7).
Об’єднанням числових проміжків називають множину, що складається з чисел, які належать хоча б одному з проміжків.
Знак 
- знак об’єднання.
Наприклад, 
(мал. 6). Зауважимо, що об’єднання проміжків не завжди є проміжком. Наприклад, множина 
не є проміжком (мал. 7).
§24. СТЕПІНЬ З РАЦІОНАЛЬНИМ ПОКАЗНИКОМ.
Означення степеня з раціональним показником.
Якщо а > 0, m - ціле число, n - натуральне число (n > 1), то виконується рівність:
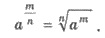
Приклад 1.
Приклад 2. Обчислити 
Розв’язання:
Властивості степеня з раціональним показником.
Властивості степеня з раціональним показником такі самі, як і властивості степеня з натуральним показником (див. § 9, п. 2).
Розглянемо застосування цих властивостей.
Приклад 1.
Приклад 2.
Приклад 3. Обчислити: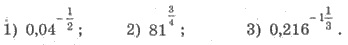 
Розв’язання.
Приклад 4. Обчислити: 
Розв’язання.
3. Перетворення виразів, які містять степінь з раціональним показником.
Приклад. 
ВІДСОТКИ.