Главная | Обратная связь

Примеры решения задач

 

Пример 1.Определить индукцию магнитного поля на оси витка с током J. Радиус витка R..

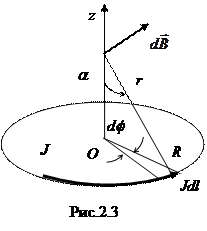Из рис.2.3 видно, что элемент тока Jdl = JRdf создает в точке наблюдения на оси Oz магнитное поле индукцией

.

В этом выражении учтено, что 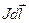^ 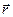. Радиальные составляющие элементарных векторов 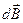, создаваемые диаметрально противоположными элементами тока, при наложении компенсируются. Поэтому результирующее поле направлено вдоль оси Оz, т.е. B = B_z. При этом

.

Тогда .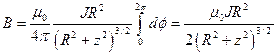

В центре витка (в точке О) z = 0 и .

 

Пример 2. Определить индукцию магнитного поля прямого проводника с током J длиной 2l с использованием принципа суперпозиции полей. Проанализировать полученный результат при l.

Из симметрии задачи следует, что отличной от нуля является лишь аксиальная составляющая индукции магнитного поля. Рассчитаем величину индукции в произвольной точке С, находящейся на расстоянии r от проводника с током. В соответствии с законом Био-Савара-Лапласа и с геометрией задачи, представленной на рис.2.4,

,

где 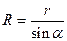. Т.к. (z - z¢) = rctga , то . Тогда

.

Выполняя интегрирование по углу от a₁ до a₂, получаем:

.

При l ® ¥ a₁ ® 0 и a₂ ® p. В этом случае .

Индукцию магнитного поля прямого проводника с током можно получить и с помощью векторного потенциала . Т.к. векторы и сонаправлены, то , где . Тогда

.

При l >> r магнитное поле и, следовательно, A_z не зависят от координаты z, т.е. A_z(z,r) = A_z(0,r). В этом случае полученное выражение для векторного потенциала существенно упрощается (положим z = 0 и учтем, что ):

.

Поскольку индукция магнитного поля связана с векторным потенциалом соотношением 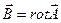, то (см. Приложение 1).

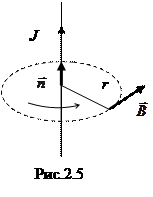Наконец, индукция магнитного поля бесконечного прямого проводника с током может быть легко определена с использованием закона полного тока. Учитывая аксиальную симметрию поля, рассмотрим циркуляцию вектора по замкнутому контуру в виде окружности произвольного радиуса r с центром на оси тока, как показано на рис.2.5. Т.к. вектор совпадает по направлению с направлением положительного обхода контура и, кроме того, зависит только от r, то

.

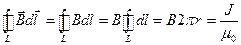Отсюда получаем .

Пример 3.Круговой виток с током лежит на плоской границе разделяя вакуума и непроводящего полупространства с магнитной проницаемостью m. Найти индукцию магнитного поля в произвольной точке на оси витка, если в отсутствие магнетика индукция магнитного поля в этой точке равна В₀.

Будем решать задачу методом токов-изображений, подобно тому, как этот прием применялся в примере 1 п.1.4.1. Т.к. ток J находится на границе, то ток-изображение J¢ совпадает с ним. Кроме того, учтем, что напряженность магнитного поля Н определяет поле токов в отсутствие магнетика, а на границе раздела в точке z = 0 выполняется равенство Н₁(0) = mН₂(0) - см. рис.2.6.

Пусть Н¢ - напряженность магнитного поля, создаваемого на оси Оz током-изображением. Тогда, как это следует из граничных условий и рис 2.6,

Н₁ = Н₀ + Н¢ и Н₂ = Н₀ - Н¢,

где Н₀ – напряженность магнитного поля витка с током в отсутствие магнетика. При z = 0

H₀(0) + H¢(0) = mH₀(0) -mH¢(0),

Откуда следует, что . Следовательно,

.

Используя результаты, полученные в примере 1этого пункта, имеем

и .

Очевидно, что отношение и не зависит от z. Поэтому для произвольной точки на оси Oz справедливо равенство . Окончательно получаем

.

 

2.1.2. Задания для самостоятельной работы

2.1.Определить индукцию магнитного поля тороидальной катушки с внешним радиусом а и внутренним – b. Число витков катушки N. По катушке протекает ток J. Проанализировать результат при увеличении внутреннего и внешнего радиусов катушки до бесконечности.

 

2.2.Определить индукцию магнитного поля коаксиального кабеля (радиус внутренней жилы кабеля а, радиус оплетки – b). По кабелю протекает ток J, пространство между жилой и оплеткой заполнено магнетиком с магнитной проницаемостью m .

 

2.3.Определить индукцию магнитного поля, создаваемого двумя бесконечными полыми коаксиальными цилиндрами радиусов a и b > a, по которым протекают одинаковые токи J в противоположных направлениях.

 

2.4.Определить индукцию магнитного поля прямого цилиндрического проводника радиуса а, по которому протекает ток J. Магнитная проницаемость материала проводника m, окружающее пространство – воздух.

2.5. По двум параллельным проводникам, расстояние между которыми 2d, протекают одинаковые токи J. Найти индукцию магнитного поля и векторный потенциал в точке, лежащей посередине прямой, соединяющей проводники. Рассмотреть случаи, когда токи сонаправлены, и когда токи направлены в противоположные стороны.

 

2.6.Рамка с током J имеет форму прямоугольника со сторонами a и b. Определить индукцию магнитного поля в геометрическом центре рамки.

 

2.7. Определить индукцию магнитного поля в точке О, если проводник с током J имеет вид, показанный на рис. Радиус изогнутой части проводника равен R, прямолинейные участки считать бесконечно длинными.

2.8. Определить индукцию магнитного поля в точке О, если проводник с током J имеет вид, показанный на рис. Радиус изогнутой части проводника равен R, прямолинейные участки считать бесконечно длинными.

2.9.Определить индукцию магнитного поля в точке О, если проводник с током J имеет вид, показанный на рис. Радиус изогнутой части проводника равен R, прямолинейные участки считать бесконечно длинными.

 

 

2.10. Ток J течет вдоль длинного прямого проводника, сечение которого имеет форму тонкого полукольца радиуса R. Найти индукцию магнитного поля в точке О.

 

 

2.11. Определить модуль и направление вектора индукции магнитного поля безграничной плоскости, по которой течет ток с линейной плотностью i.

 

2.12. Внутри длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость. Оси провода и полости совпадают. Радиус полости а, радиус провода b > a. Определить индукцию магнитного поля провода, если по нему протекает постоянный ток плотности j.

 

2.13. Внутри длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена на вектор . Радиус полости а, радиус провода b > 2a. Определить индукцию магнитного поля в полости и на оси провода, если по нему протекает постоянный ток плотности j.

2.14.Расстояние между двумя параллельными линейными проводниками с одинаковыми однонаправленными токами J равно 2d. Определить индукцию магнитного поля в точке, равноудаленной от проводников на расстояние b > 2d.

 

2.15.Заряд q равномерно распределен по объему непроводящего однородного шара радиуса R. Шар равномерно вращается вокруг оси, проходящей через его центр, с угловой скоростью w. Найти магнитный момент шара.

 

2.16.Тонкая непроводящая сфера равномерно заряжена по поверхности зарядом q. Радиус сферы R. Сфера равномерно вращается вокруг оси, проходящей через ее центр, с угловой скоростью w. Найти магнитный момент сферы.

2.17.Для условия задачи 2.16найти индукцию магнитного поля в центре сферы.

 

2.18.Тонкий непроводящий диск радиуса R равномерно заряжен с поверхностной плотностью заряда s. Диск вращается вокруг своей оси с постоянной угловой скоростью w. Определить магнитный момент диска.

 

2.19. Для условия задачи 2.18найти индукцию магнитного поля в центре диска.

 

2.20.Два длинных параллельных провода с пренебрежимо малыми сопротивлениями с одного конца замкнуты на сопротивление R, а с другого конца подключены к источнику постоянного напряжения. Расстояние между осями проводов в h раз больше радиуса сечения каждого провода. При каком значении сопротивления R результирующая сила взаимодействия между проводами обращается в нуль?

 

2.21.Постоянный ток J течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса R (см. рис. к задаче 2.10). Такой же ток течет в противоположном направлении по тонкому проводнику, расположенному на оси первого проводника. Найти силу взаимодействия проводников в расчете на единицу их длины.

 

2.22.Индукция магнитного поля в вакууме вблизи плоской поверхности однородного изотропного магнетика равна В, причем вектор 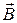составляет угол a с нормалью к поверхности. Магнитная проницаемость магнетика равна m. Найти модуль вектора индукции B¢ магнитного поля в магнетике вблизи поверхности.

 

2.23.Для условия задачи 2.22 найти поток вектора через поверхность сферы радиуса R, центр которой лежит на поверхности магнетика.

 

2.24.Для условия задачи 2.22 найти циркуляцию вектора 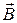по квадратному контуру со стороной l, расположенному так, как показано на рис.

 

2.25. Система состоит из двух параллельных плоскостей, по которым протекают параллельные токи в противоположных направлениях с линейной плотностью i. Определить индукцию магнитного поля между плоскостями и вне плоскостей. Как направлен вектор магнитной индукции?

 

2.26.Бесконечно длинный прямой соленоид с током наполовину заполнен магнетиком, как показано на рис. Представить качественные графики магнитной индукции В, напряженности магнитного поля Н и намагничения I на оси соленоида в зависимости от х.