 |
|
Краткие теоретические сведения
Квазистационарные явления связаны с достаточно медленно изменяющимися электромагнитными полями такими, что токи проводимости значительно превышают токи смещения:
 пр >>
пр >>  см . (3.1)
см . (3.1)
Условие (3.1) выполняется в области частот w << g/eо. Для проводников (g ~ 107 Ом-1×м-1)
условие (3.1) выполняется вплоть до частот w ~ 1013 Гц. На практике к квазистационарным явлениям относят переменные электромагнитные поля, период колебаний которых много больше времени распространения поля через систему токов:
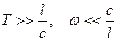 . (3.2)
. (3.2)
В области квазистационарных явлений уравнения Максвелла имеют вид:
1) 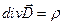 , 3)
, 3)  ,
,
2) 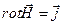 , 4)
, 4)  . (3.3)
. (3.3)
Введение скалярного j и векторного  потенциалов
потенциалов
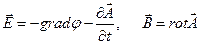 (3.4)
(3.4)
позволяет перейти от системы четырех уравнений (3.3) к системе из двух уравнений
 . (3.5)
. (3.5)
Система уравнений Пуассона (3.5) отражает тот факт, что в данный момент времени распределение полей в системе определяется распределением зарядов и токов в этот же момент времени. Приведенное утверждение означает применимость правил Кирхгофа для разветвленных цепей переменного тока.
Учет электромагнитной индукции (уравнение 4) в системе (3.3)) приводит к закону Ома в замкнутом линейном контуре в виде:
 . (3.6)
. (3.6)
В случае разветвленной цепи (системы контуров) для каждой из ветвей можно записать:
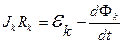 . (3.7)
. (3.7)
Если имеется несколько индуктивно связанных контуров, то поток Фk, пронизывающий k-тый контур, равен
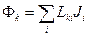 , (3.8)
, (3.8)
где Lki – коэффициент взаимной индукции между i-тым и k-тым контурами, Lkk - коэффициент самоиндукции k-го контура.
В замкнутой цепи с ЭДС e(t), емкостью С, индуктивностью L и сопротивлением R в квазистационарном приближении ток J удовлетворяет дифференциальным уравнениям:
 (3.9)
(3.9)
При гармонической зависимости ЭДС от времени 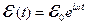
 , (3.10)
, (3.10)
где i – мнимая единица, Z - комплексное сопротивление цепи, R – активное сопротивление и X – реактивное сопротивление. В свою очередь
 . (3.11)
. (3.11)
При этом фазовый сдвиг j между током и напряжением на участке цепи определяется как
 . (3.12)
. (3.12)
Следует помнить, что правила расчетов полного комплексного сопротивления формально совпадают с известными правилами последовательного и параллельного соединений сопротивлений, конденсаторов и катушек индуктивности.