Главная | Обратная связь

П.1.2. Цилиндрические координаты

Положение точки М с декартовыми координатами x,y,z в цилиндрических координатах описывается тремя независимыми числами (рис. П.1.):

- расстоянием r (r 0) от оси Oz до точки М (проекцией радиус-вектора точки М на

плоскость xOy);

- углом f ( ) между осью Ох и проекцией на плоскость хОу;

- проекцией z радиус-вектора точки М на ось Оz ( ).С координатами r, f и z связана тройка ортогональных единичных векторов и .

При этом декартовы координаты x, y, z точки М связаны с ее цилиндрическими координатами соотношениями:

Элементы длины, площади и объема в цилиндрических координатах имеют вид:

,

.

Операторы теории поля записываются в цилиндрических координатах следующим образом:

;

;

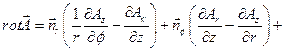
Оператор Лапласа в цилиндрических координатах имеет вид:

,

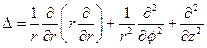или .

 

П.1.3. Сферические координаты

В сферических координатах (рис. П.2) положение точки М в пространстве определяется тремя числами , где - расстояние от начала координат до точки, т.е. ( ³0); - угол между осью Oz и радиус-вектором точки (0 £ £ p), - угол между осью Ох и проекцией радиус-вектора точки на плоскость хОу (0 £ < 2p).

Декартовы и сферические координаты связаны между собой соотношениями

, .

С координатами r, q и f связана правая тройка единичных ортогональных векторов

.

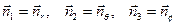Элементы длины, площади и объема в сферических координатах имеют следующий вид:

.

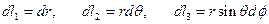
Векторные соотношения в сферических координатах:

градиент скалярной функции j

,

дивергенция векторной функции

,

ротор векторной функции

.

Оператор Лапласа в сферических координатах имеет вид:

.

В некоторых случаях оператор Лапласа записывают так: , где

- его радиальная часть, а

- угловая часть.

В центрально-симметричном поле, распределение которого не зависит от углов и , , т.е. такое поле описывается одномерным оператором Лапласа .