Примеры решения задач

Пример 12. 1. В пространстве, наполовину заполненном парафином (ε₂=2), создано однородное электрическое поле, напряжённость которого в вакууме Е₁=4В/м. Вектор образует с плоской границей вакуум – парафин угол α=60º. Определите в парафине: 1) электрическое смещение D₂; 2) напряжённость Е₂ электростатического поля; 3) поляризованность Р₂.

Дано: ε₂=2; Е₁=4В/м; α=60º; ε₁=1.

Найти: 1) D₂; 2) Е₂; 3) Р₂.

Решение. Поскольку в задаче задан вектор как по модулю, так и по направлению (рис.а), то задано и направление вектора в вакууме (рис.б) (векторы и параллельны).

Связь между нормальной и тангенциальной составляющими векторов и :

D_n=ε₀εE_n и D_τ=ε₀εE_τ (1)

При переходе через границу раздела тангенциальная составляющая вектора (E_τ) и нормальная составляющая вектора (D_n) не претерпевают скачка, т.е.

Е_τ₁=E_τ₂; D_n₁= D_n₂(2)

а нормальная составляющая вектора (E_n) и тангенциальная составляющая вектора (D_τ)

; (3)

что схематически изображено на рисунках.

Из формулы (3), учитывая, что ε₁=1, получим

Е_τ₁=ε₂E_n₂ и (4)

Из рисунка б, с учётом формул (1) и (4), следует, что

В вакууме (см.рис. б) D_n₁= D₁sinα=ε₀E₁sinα, D_τ₂= D₁cosα=ε₀E₁cosα.

Тогда искомое электрическое смещение в парафине

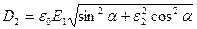
Из рисунка а, с учётом формул (1) и (4), следует, что

В вакууме (см.рис. а) Е_n₁= Е₁sinα; Е_τ₁= Е₁cosα.

Тогда искомая напряжённость электростатического поля в парафине

Поляризованность связана с и соотношением

откуда следует, что вектор в парафине направлен так же, как вектор (или ). Тогда искомая поляризованность в парафине

P₂=D₂-ε₀E₂

Ответ: 1) D₂=46 пКл/м²; 2) Е₂=2,6 В/м; 3) Р₂=23 пКл/м².

Пример 12. 2. Между обкладками плоского конденсатора, заряженного до разности потенциалов 1,5кВ, зажата парафиновая пластинка (ε=2) толщиной 5 мм. Определите поверхностную плотность связанных зарядов на парафине.,

Дано: U=1,5кВ=1,5∙10³В; ε=2; d=5мм=5∙10^-3м.

Найти: σ'.

Решение. Векторы , и связаны соотношением

= ε₀ +

где и - соответственно векторы электрического смещения и напряжённости поля плоского конденсатора; - вектор поляризованности диэлектрика. Так вектора и нормальны к поверхности диэлектрика, то D_n=D и Е_n=Е. тогда можем записать D= ε₀Е+Р; где Р= σ', т.е. равна поверхности плотности связанных зарядов диэлектрика (учли, что Р_n=Р). Тогда

σ'=D- ε₀Е.

Учитывая, что D= ε₀Е и , где d – расстояние между обкладками конденсатора, найдём

σ'= ε₀(ε-1)Е= ε₀(ε-1) .

Ответ: σ' =2,65 мкКл/м².

Пример 12. 3. Плоский конденсатор, между обкладками которого находится стеклянная пластинка (ε=7)толщиной d=3мм, заряжен до разности потенциалов U=500В. Определите: 1) поверхностную плотность σ зарядов на обкладках конденсатора; 2) поверхностную плотность σ' связанных зарядов на стекле. Величиной зазора между пластинкой и обкладками пренебречь.

Дано: ε=7; d=3мм=3∙10^-3м; U=500 В;

Найти: 1) σ; 2) σ'

Решение. Напряжённость поля внутри конденсатора при наличии диэлектрика между его обкладками

. (1)

С другой стороны, напряжённость электрического поля внутри конденсатора

(2)

Приравняв (1) и (2), получим искомую поверхность плотность зарядов на обкладках конденсатора

Поверхностная плотность σ' связанных зарядов равна поляризованности Р: σ'=Р. Поляризованность диэлектрика Р и напряжённости Е электростатического поля связаны соотношением Р=χ ε₀Е, где χ- диэлектрическая восприимчивость диэлектрика, связанная с диэлектрической проницаемостью соотношением:

ε=1+ χ. Тогда, учитывая формулу (2), получим искомую поверхностную плотность зарядов:

σ' =P= χ ε₀Е= ε₀(ε-1)Е =ε₀(ε-1)

Ответ:1) σ =10,3 мкКл; 2) σ' =8,85 мкКл

Пример 12. 4. Расстояние между обкладками плоского конденсатора

d =1мм. После зарядки конденсатора до разности потенциалов U=700В между обкладками вставили стеклянную пластинку (ε=7). Определите: 1) диэлектрическую восприимчивость χ стекла; 2) поверхностную плотность σ' связанных зарядов на стеклянной пластинке.

Дано: d=1мм=1∙10^-3м; U=700 В; ε=7.

Найти: 1) χ; 2) σ'

Решение. Связь диэлектрической проницаемости ε и диэлектрической восприимчивость χ

ε=1+ χ

откуда искомая

χ= ε -1

Напряжённость поля внутри конденсатора после его зарядки

(1)