 |
|
Исследование сходимости рядов.
Во многих случаях исследование сходимости рядов сводится к вычислению некоторых пределов и сравнению их значений с некоторыми заданными числами (или символом ∞). Так будет, если для исследования сходимости ряда используются предельный признак сравнения, признак Даламбера, признак Коши (с радикалом) и некоторые другие признаки. Рассмотрим примеры.
ПРИМЕР 2.6.
Исследовать сходимость ряда  .
.
При больших n , 

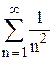 . Воспользуемся предельным признаком сравнения, сравнив данный ряд с рядом
. Воспользуемся предельным признаком сравнения, сравнив данный ряд с рядом 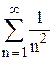 . Ряд
. Ряд 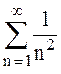 сходится, как ряд Дирихле
сходится, как ряд Дирихле  с параметром p > 1. С помощью приложения Mathcad найдём предел отношения общих членов этих рядов. Для этого нужно набрать:
с параметром p > 1. С помощью приложения Mathcad найдём предел отношения общих членов этих рядов. Для этого нужно набрать:
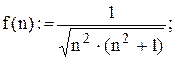
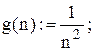


Итак, предел отношения общих членов рассматриваемых рядов конечный и не равный нулю (равен 1). Следовательно, в отношении сходимости оба ряда ведут себя одинаково, т.е. исследуемый ряд сходится.
Аналогично можно использовать приложение Mathcad, при иссле-довании сходимости ряда с помощью признака Даламбера ( 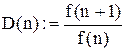 ) и признака Коши (
) и признака Коши (  ).
).
Заметим, что Windows приложение Mathcad позволяет вычислять не все пределы, а только те, вычисление которых программно обеспечено в этом приложении.
Приложение Mathcad позволяет вычислять значения многих несобственных интегралов. Это можно использовать при исследовании сходимости рядов с помощью интегрального признака Коши.
ПРИМЕР 2.7.
Исследовать сходимость ряда 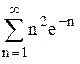 .
.
Функция  имеет производную
имеет производную 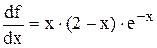 , которая при x > 2 отрицательная,
, которая при x > 2 отрицательная, 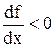 . Тогда эта функция определена, непрерывна, неотрицательная и убывающая на промежутке [2 ; +∞) и, по интегральному признаку Коши, ряд
. Тогда эта функция определена, непрерывна, неотрицательная и убывающая на промежутке [2 ; +∞) и, по интегральному признаку Коши, ряд  и интеграл
и интеграл  либо оба сходятся, либо оба расходятся . Вычислим этот интеграл с помощью ЭВМ. Для этого нужно набрать:
либо оба сходятся, либо оба расходятся . Вычислим этот интеграл с помощью ЭВМ. Для этого нужно набрать:
 .
.
Интеграл имеет конечное значение, следовательно, сходится. Тогда исследуемый ряд тоже сходится.
3. ОБРАЗЦЫ ВЫПОЛНЕНИЯ НЕКОТОРЫХ ЗАДАНИЙ
Рассмотрим решения некоторых, наиболее трудных, практических заданий.
Задание 3
Найти сумму числового ряда  .
.
Разложим дробь 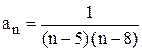 на простейшие дроби.
на простейшие дроби.

Найдём А и В, решив систему уравнений

Итак, А = 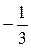 , В =
, В =  , и а n =
, и а n =  .
.
Тогда частичная сумма данного ряда S к = а9 + a10 + … + a к =

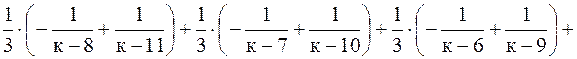
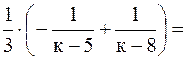
 , и
, и
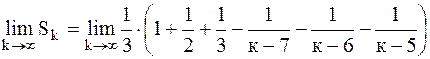 =
= 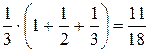 .
.
Итак, существует конечный предел последовательности частичных сумм S k . Следовательно, по определению, ряд сходится и его сумма равна  .
.
Задание 8
Исследовать на сходимость (абсолютную и условную) знакочере-дующийся ряд  .
.
Исследуем ряд на абсолютную сходимость. Для этого рассмотрим ряд составленный из модулей членов данного ряда  . Сравним его с рядом
. Сравним его с рядом 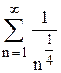 , отметив, что:
, отметив, что:
оба ряда с неотрицательными членами ;
второй ряд расходится, как ряд Дирихле с параметром р < 1 (p =  );
);
для n > 2 выполняются неравенства ln n > 1,  .
.
Тогда по признаку сравнения рядов с неотрицательными членами ряд  расходится , а это означает, что исследуемый ряд
расходится , а это означает, что исследуемый ряд  не сходится абсолютно.
не сходится абсолютно.
Для исследования данного ряда на условную сходимость применим признак Лейбница, отметив, что :
данный ряд знакочередующийся;
предел общего члена ряда ( модуля общего члена ряда ) равен 0 (действительно, используя правило Лопиталя, имеем
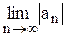 =
= 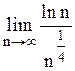 =
= 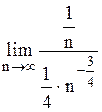 =
= 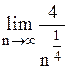 = 0 );
= 0 );
начиная с некоторого номера члены ряда убывают по абсолютной величине ( действительно, функция  имеет производную
имеет производную 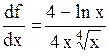 , которая отрицательна, если x >
, которая отрицательна, если x > 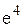 ).
).
Тогда по признаку Лейбница данный ряд сходится условно.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Понятия числового ряда, частичной суммы и остатка ряда, сходимости и суммы ряда.
2. Приближенное вычисление суммы ряда и оценка погрешности.
3. Операции над рядами (сумма и разность рядов, произведение ряда на число, произведение рядов). Теоремы о сходимости суммы и разности рядов, произведения ряда на число, произведения рядов.
4. Критерий Коши сходимости числового ряда.
5. Необходимые признаки сходимости рядов ( два признака: в терминах членов ряда и частичных сумм ряда). Привести примеры, показывающие, что эти признаки не являются достаточными признаками сходимости.
6. Определение гармонического ряда. Почему этот ряд называется гармоническим? Что можно сказать о сходимости этого ряда?
7. Сформулировать признаки сравнения для рядов с положительными членами.
8. Сформулировать признак Даламбера. Привести примеры.
9. Сформулировать признак Раабе.
10. Сформулировать признак Коши с радикалом. Привести примеры.
11. Сформулировать интегральный признак Коши. Применить этот признак к исследованию сходимости гармонического ряда.
12. Обобщённый гармонический ряд или ряд Дирихле (определение). Что можно сказать о сходимости обобщённого гармонического ряда при различных действительных значениях параметра?
13. Знакопеременные ряды. Определение абсолютной сходимости ряда. Теорема об абсолютной сходимости ряда.
14. Знакочередующиеся ряды. Сформулировать признак Лейбница. Оценка остатка ряда Лейбница.
15. Определение условной сходимости знакопеременного ряда. Привести примеры.
16. Свойства абсолютно и условно сходящихся рядов.
17. Сформулировать признак Абеля-Дирихле. Привести пример.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. М.: Наука,1984. 432с.
2. Ефимов А.В. Математический анализ ( специальные разделы ).Ч.1. Общие функциональные ряды и их приложение. М.: Высшая школа, 1980. 279с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления.Т.2. М.: Наука, 1978. 576с.
4. Кудрявцев Л.Д. Курс математического анализа. Т.1. М.:Высшая школа, 1981. 687с.
5. Бугров Я.С., Никольский С.М. Высшая математика: Задачник. М.: Наука, 1987. 256с.
6. Сборник задач по математике для втузов. Ч.2. Специальные разделы математического анализа / Под ред. А.В. Ефимова и Б.П. Демидовича. М.: Наука, 1986. 368с.
7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2-х ч. Ч.1. М.: Высшая школа,1996. 416с.
8. Запорожец Г.И. Руководство к решению задач по математическому анализу. М.: Высшая школа, 1983. 460с.
9. Шмелёв Т.А. Теория рядов в задачах и упражнениях. М.: Высшая школа, 1983. 176с.
10. Выгодский М.Я. Справочник по высшей математике для ВУЗов и ВТУЗов. М.: ВЕК, Большая Медведица, 1997. 863с.
11. Ряды и их приложения: Методические указания для студентов, обуча-ющихся по системе дистанционного образования / Курск. гос. техн. ун-т; Сост.: И.Н. Росляков, Е.В. Селезнёва. Курск, 2000. 49с.
12. MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчёты в среде WINDOWS 95: Пер. с анг. М.: Информационно-издательский дом "Филин", 1996. 712с.