 |
|
ДИСЦИПЛИНА «АЛГЕБРА И ГЕОМЕТРИЯ»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
МЕЖДУНАРОДНАЯ АКАДЕМИЯ БИЗНЕСА
КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
УТВЕРЖДАЮ
Проректор по академическим вопросам
_____________________ Дуйсенгулова Н.С.
«____»___________________2012 г.
Образовательная программа – бакалавриат
Специальность: 5B070300 «Информационная система»
Форма обучения - очная
СИЛЛАБУС
По дисциплине «Алгебра и геометрия»
Курс – 1
Семестр – 1
Количество кредитов – 3
Преподаватель кафедры ИТ –Дюсембаева Р.М.
Телефон: 8 771 450 62 05, кабинет №119
АЛМАТЫ – 2012
Составитель: Дюсембаева Р.М.
Силлабус составлен в соответствии с рабочей программой курса «Алгебра и геометрия» для специальности 5В090900 «Информационная система».
Силлабус рассмотрен на заседании кафедры Информационных технологий от
_____________________ 2012 г., протокол №____
Зав. кафедрой, д.т.н.,профессор _________________________ Бельгибаев Б.А.
Силлабус утвержден на заседании УМС МАБ
Протокол №_____ от «____»_______________2012 г.
ДИСЦИПЛИНА «АЛГЕБРА И ГЕОМЕТРИЯ»
Данные о преподавателе: Дюсембаева Раушан Мейрбековна –м.е.н., преподаватель кафедры «Информационные системы». Имеет ряд публикаций.
Контактные телефоны: кафедра «Информационные системы» - тел.302-21-27, ул. Розыбакиева,227 каб.119
Пререквизиты дисциплины: Знание школьного курса математики, особенно алгебры и
арифметики, основные понятия физики, информатики.
Постреквизиты дисциплины: Все дисциплины экономического и инженерного тома, в том числе математический анализ, дискретная математика, кибернетика, экономическая теория. Описание дисциплины: На основании нового Государственного стандарта предложенный курс позволяет обучать студентов необходимому математическому аппарату для усвоения далее инженерных и экономических дисциплины, развивать творческие способности студентов путем расширения самостоятельной работы.
Краткое описание дисциплины:Основные разделы предмета «Алгебра и геометрия »:
- системы линейных алгебраических уравнений;
- векторная алгебра;
- Евклидовые пространства;
- линейные операторы в линейном пространстве;
- линейные геометрические объекты;
- кривые и поверхности второго порядка;
- квадратичные формы.
Цели изучения дисциплины:
В результате изучения курса математики студент должен:
- иметь представление о методах математики, ее роль в развитии технических наук, где и как
- применяются математические методы;
- знать основные определения, теоремы, правила, математические методы и практические применения;
- приобрести практические навыки в решении задач на все предусмотренные программой темы курса;
- решений задач на все предусмотренные программой темы курса;
- развить умение и способности самостоятельно пополнять свое образование
Задачи изучения дисциплины: «Алгебра и геометрия» в системе подготовки бакалавра по информационным системам, вычислительной техники и программное обеспечение:
- освоение математического аппарата помогающего моделировать, анализировать и решать прикладные задачи, в случае необходимости с использованием компьютерной техники;
- помочь студентам усвоить математические методы, дающие возможность изучать и прогнозировать процессы и явления из области будущей деятельности студентов как специалистов;
- формировать умения и навыки самостоятельного анализа исследования проблем информационных систем, развивать стремление к научному поиску путей совершенствования своей работы.
Задачи изучения дисциплины состоят в том, чтобы студент
Знал:
- теоретические основы (основные определения, теоремы, правила, методы) математики;
- приемы исследования и решения математически сформулированных задач;
- области применения полученых математических знаний;
- простейшие численные методы;
Умел:
- уточнять постановку задачи,
- выбирать метод решения поставленной задачи,
- решить и интерпретировать полученные результаты, разрабатывать рекомендации на их основе;
- самостоятельно изучать математическую литературу;
Приобрел навыки самостоятельного анализа исследования экономических проблем,практические навыки решения задач, предусмотренных программой; развивать стремление к научному поиску путей совершенствованиясвоей работы.
Компетенции:
-владение приемами исследования и решения математической модели практических задач;
-умение анализировать, логически мыслить;
-владение вычислительными навыками, использование различных методов вычисления.
КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № | Наименование темы | Распределение по неделям | |||
| Лекции | Практические занятия | СРС | СРСП | ||
| Матрицы и определители Матрицы, действия над ними. Матрицы и их свойства. Обратная матрица. Ранг матрицы. | |||||
| Определители. Определители второго и третьего порядков. Свойства определителей. Миноры и алгебраические дополнения. Теорема Лапласа. | |||||
| Системы линейных алгебраических уравнений. Системы линейных алгебраических уравнении. Метод Гаусса. Решение матричных уравнений. | |||||
| Фундаментальная система в решении системы линейных алгебраических уравнений. Фундаментальная система в решении системы линейных алгебраических уравнений. | |||||
| Векторная алгебра. Пространства R и R3. Линейные операции над векторами. Линейные пространства. Линейно-независимые системы векторов. Базис. Декартово система координат в пространствах R2 , R3 и Rn. | |||||
| Применение векторам нелинейных преобразовании. Скалярное произведения векторов в R3 . Векторное произведение векторов. Смешанное произведение и его свойства. | |||||
| Евклидовые пространства. Разложение вектора по базису в евклидовом пространстве. Ортогональный базис. Теорема Шмидта об ортогонализации базиса. | |||||
| Рубежный контроль 1 7 | |||||
| Линейный оператор в линейным пространстве. Линейный оператор в заданном базисе в пространстве R2, R3 и Rn. Сопряженный оператор. Сопряженная матрица. Ортогональная матрица. Ядро и область значений линейного оператора. | |||||
| Линейные геометрические объекты. Прямая линия. Угол между прямыми. Взаимно расположении прямых. | |||||
| Прямые пространстве. Различные уравнения плоскости и прямой в R . Взаимное расположение прямой и плоскости в R3. Полупространства. Приложения уравнения прямой в пространстве и уравнения плоскости. | |||||
| Плоскости в Rn. Плоскости в Rn. Полупространства и система полупространств в Rn. | |||||
| Кривые второго порядка. Общее уравнение кривой второго порядка. Канонические уравнения эллипса. Канонические уравнения гиперболы, параболы. | |||||
| Геометрических свойств кривых. Геометрических свойств кривых. Технические приложения геометрических свойств кривых. | |||||
| Поверхности второго порядка. Поверхности второго порядка. Канонические формы уравнений. Исследование поверхностей второго порядка методом сечений. | |||||
| Квадратичные формы. Квадратичные формы. Канонические виды квадратичных форм в Rn и их приложения. | |||||
| Рубежный контроль 2 15 | |||||
| Экзаменационная сессия 16-18 |
Содержание практических занятий, форма контроля и оценка
| № темы | Вопросы практических занятий | Литература | Форма контроля | Макс. балл |
| Действия над матрицами. | №1-8 ч.1, с.32-37 | Проверка д/з | ||
| Определители второго и третьего порядков.Теорема Лапласа. | №1-8 ч.1, с.32-37 | ИДЗ 1 | ||
Решения системы
уравнений  .
Матричный метод
Формулы Крамера, метод Гаусса .
Матричный метод
Формулы Крамера, метод Гаусса
| №5-8 с.199;№7 с.18; №8 с.21 | Контрольная работа | ||
| Методы решения системы линейных алгебраических уравнений. | №4 ч.1, с.88 | Самостоятельная работа | ||
| 1.Расстояние между двумя точками. Деление отрезка в данном отношении. 2.Векторы. Операции над векторами. | №1-8 ч.1, с.90 | коллоквиум | ||
| Скалярное, векторное, смешанное произведения векторов. | №1-8 ч.1 с.90 | Решение задач | ||
| Базис. Разложение вектора по базису в евклидовом пространстве. | №3 с.46-50; №4 ч.1, №3 с.48- | тестирование | ||
| Линейные операторы в Rn. Собственные векторы и собственные значения линейных операторов в R2 , R3 и Rn . | 55; №4 ч.1 | |||
| Прямая на плоскости. Их взаимные расположения. Полуплоскости и система полуплоскостей. | №1-8 с.66; №4ч.1, №7,8 | Рубежный контроль | ||
| Различные уравнения плоскости и прямой в пространстве. Их взаимно расположения. | №3 с.78 | Проверка д/з | ||
| Полупространства. Выпуклые множества. | №4 ч.2, с.222 | тестирование | ||
| Кривые второго порядка на плоскости. Их приложения | №7.8 №4 ч.2, с.208-219 | Самостоятельная работа | ||
| Геометрических свойств кривых. | 1-5,9,11 | Решение задач, устный опрос | ||
| Поверхности второго порядка. Их приложения. | 2-11 | Решение задач | ||
| Квадратичные формы R2 и R3 и Rn. Геометрические приложения квадратичных форм в R2 и R3 . | 2-11 | Конспект. Устный опрос. |
ГРАФИК ПРОВЕДЕНИЯ СРСП*
| № темы | Задания на СРС | Литература | Форма контроля | Сроки сдачи (неделя) | Макс. балл |
| Решение тестовых заданий | 1-3,  ч.1, с.32-37 ч.1, с.32-37
| тестирование | |||
| Выполнение ИДЗ | №4 ч.1, с.32-37 | Защита ИДЗ | |||
| Применение элементов линейной алгебры в экономике | №1,2,3,9 | Защита СРС | |||
| Решение задач | 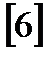 , с.6-35
7,8 , с.6-35
7,8
| Письменная работа | |||
| Решение тестовых заданий | 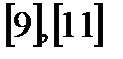 с.7-11 с.7-11
| Задания по карточкам | |||
| Подготовка к контрольной работе. |  ч.1, ч.1,
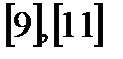
| тестирование | |||
| Базис. Разложение вектора по базису в евклидовом пространстве. | №1,2;7,8 | Проверка конспекта | |||
| Решение задач | №3 с.66; №4ч.1, №7,8 | Проверка тетрадей | |||
| Выполнение ИДЗ | №1,2,3,9 | Защита СРС | |||
Разбор материала по 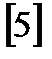 ч.2, с.208-219 ч.2, с.208-219
|  ч.2, с.208-219 ч.2, с.208-219
| Устный опрос | |||
| Решение задач. | №7.8 №4 ч.2, с.208-219 | Проверка тетрадей | |||
| Выполнение ИДЗ |  ч.2, с.137-159 ч.2, с.137-159
| Защита ИДЗ | |||
| Подготовка к контрольной работе. | №1,2,3,9 | Проверка конспекта | |||
| Решение задач. |  ч.2, 7,8 ч.2, 7,8
| Контрольная работа | |||
| Конспект по теме | №1,2,3,9,10,11 | Устный опрос |
* Примечание: Контроль и оценка выполнения заданий СРС осуществляется на занятиях СРСП.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная литература
1. Вугров Я.С., Никольский С.М. Элементу линейной алгебры и аналитической геометрии. – М.,: Наука, 1988г.
2. Ильин В. А., Позняк Э.Г., Линейная алгебра, M:Наука. 1983 г.
3. Красс М.С., Чупрынов Б.П., Основы математики и ее приложения в экономическом образовании. М.,2000г.
4 Сборник индивидуальных заданий по высшей математике. Под ред.А.П.Рябушко.Минск, В.ш., 1990. Ч.1,2,3 (более поздние переиздания)
5 Математика для экономистов. Под ред. Кельтеновой Р.Т. Экономика ,2000г.
6.Казешев А.К., Нурпеисов С.А. Сборник задач по высшей математике для экономистов. Алматы,2001г.
7.Тестовые задания по математике для экономистов. Под ред. Рахметовой Р.У. –Алматы:КазЭУ, 2007. -44с.
8*.Задания к практикуму по высшей математике. Метод.пособие. Составитель Скаков С.Б. Алматы, 2004, 33 с.
Дополнительная литература
9.Шипачев В.С. Высшая математика. М.:Высшая школа, 1990
10.Кельтенова Р.Т., Шумаева О.В. Высшая математика для экономистов. Сборник тестовых заданий. − Алматы: Алматинская академия экономики и статистики, 2004.
11. Красс М.С. Математика для экономических специальностей. М., 1998г.