Главная | Обратная связь

Совершенные и квазисовершенные коды

Групповой -код, исправляющий все ошибки веса, не большего 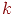, и никаких других, называется совершенным.

Свойства совершенного кода¹⁾:

1. Для совершенного -кода, исправляющего все ошибки веса, не большего 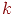, выполняется соотношение 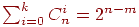. Верно и обратное утверждение;
2. Совершенный код, исправляющий все ошибки веса, не большего 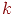, в столбцах таблицы декодирования содержит все слова, отстоящие от кодовых на расстоянии, не большем 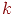. Верно и обратное утверждение;
3. Таблица декодирования совершенного кода, исправляющего все ошибки в не более чем 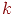позициях, имеет в качестве лидеров все строки, содержащие не более 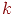единиц. Верно и обратное утверждение.

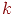
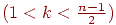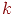Совершенный код - это лучший код, обеспечивающий максимум минимального расстояния между кодовыми словами при минимуме длины кодовых слов. Совершенный код легко декодировать: каждому полученному слову однозначно ставится в соответствие ближайшее кодовое. Чисел , и , удовлетворяющих условию совершенности кода очень мало. Но и при подобранных , и совершенный код можно построить только в исключительных случаях.

Если , и 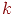не удовлетворяют условию совершенности, то лучший групповой код, который им соответствует называется квазисовершенным, если он исправляет все ошибки кратности, не большей 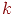, и некоторые ошибки кратности . Квазисовершенных кодов также очень мало.

Двоичный блочный -код называется оптимальным, если он минимизирует вероятность ошибочного декодирования. Совершенный или квазисовершенный код - оптимален. Общий способ построения оптимальных кодов пока неизвестен.

Для любого целого положительного числа существует совершенный -код, исправляющий одну ошибку, называемый кодом Хэмминга (Hamming), в котором 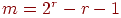и .

Действительно, .

Порядок построения кода Хэмминга следующий:

1. Выбираем целое положительное число . Сообщения будут словами длины 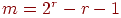, а кодовые слова - длины ;
2. В каждом кодовом слове бит с индексами-степенями двойки - являются контрольными, остальные - в естественном порядке - битами сообщения. Например, если , то биты - контрольные, а - из исходного сообщения;
3. Строится матрица из строк и столбцов. В -ой строке стоят цифры двоичного представления числа . Матрицы для r=2, 3 и 4 таковы:
4. Записывается система уравнений , где - матрица из предыдущего пункта. Система состоит из уравнений. Например, для :

1. Чтобы закодировать сообщение 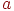, берутся в качестве , не равно степени двойки, соответствующие биты сообщения и отыскиваются, используя полученную систему уравнений, те , для которых - степень двойки. В каждое уравнение входит только одно , . В выписанной системе входит в 1-е уравнение, 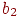- во второе и - в третье. В рассмотренном примере сообщение будет закодировано кодовым словом .

Декодирование кода Хэмминга проходит по следующей схеме. Пусть принято слово , где - переданное кодовое слово, а 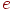- строка ошибок. Так как , то . Если результат нулевой, как происходит при правильной передаче, считается, что ошибок не было. Если строка ошибок имеет единицу в -й позиции, то результатом произведения будет -я строка матрицы или двоичное представление числа . В этом случае следует изменить символ в -й позиции слова , считая позиции слева, с единицы.

Пример. 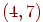-код Хэмминга имеет в качестве одного из кодовых слов . Матрица приведена на шаге 3 хода построения кода Хэмминга. Ясно, что . Добавим к строку ошибок . Тогда и , т.е. ошибка находится в третьей позиции. Если , то 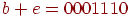и позиция ошибки - и т.п. Если ошибка допущена в более чем в одной позиции, то декодирование даст неверный результат.

Код Хэмминга - это групповой код.

Это следует из того, что -код Хэмминга можно получить матричным кодированием, при помощи -матрицы, в которой столбцы с номерами не степенями 2 образуют единичную подматрицу. Остальные столбцы соответствуют уравнениям шага 4 построения кода Хэмминга, т.е. 1-му столбцу соответствует уравнение для вычисления 1-го контрольного разряда, 2-му - для 2-го, 4-му - для 4-го и т.д. Такая матрица будет при кодировании копировать биты сообщения в позиции не степени 2 кода и заполнять другие позиции кода согласно схеме кодирования Хэмминга.

Пример. Кодирующая матрица для 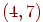-кода Хэмминга -

Ее столбцы с номерами 3, 5, 6 и 7 образуют единичную подматрицу. Столбцы с номерами 1, 2 и 4 соответствуют уравнениям для вычисления контрольных бит, например, уравнению соответствует столбец 1101, т.е. для вычисления первого контрольного разряда берутся 1, 2 и 4 биты исходного сообщения или биты 3, 5 и 7 кода.

К -коду Хэмминга можно добавить проверку четности. Получится 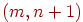-код с наименьшим весом ненулевого кодового слова 4, способный исправлять одну и обнаруживать две ошибки.

Коды Хэмминга накладывают ограничения на длину слов сообщения: эта длина может быть только числами вида : 1, 4, 11, 26, 57, Но в реальных системах информация передается байтам или машинными словами, т.е. порциями по 8, 16, 32 или 64 бита, что делает использование совершенных кодов не всегда подходящим. Поэтому в таких случаях часто используются квазисовершенные коды.

Квазисовершенные -коды, исправляющие одну ошибку, строятся следующим образом. Выбирается минимальное так, чтобы

Каждое кодовое слово такого кода будет содержать контрольных разрядов. Из предыдущих соотношений следует, что

Каждому из разрядов присваивается слева-направо номер от 1 до . Для заданного слова сообщения составляются 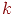контрольных сумм по модулю 2 значений специально выбранных разрядов кодового слова, которые помещаются в позиции-степени 2 в нем: для выбираются разряды, содержащие биты исходного сообщения, двоичные числа-номера которых имеют в -м разряде единицу. Для суммы это будут, например, разряды 3, 5, 7 и т.д., для суммы - 3, 6, 7 и т.д. Таким образом, для слова сообщения будет построено кодовое слово . Обозначим сумму по модулю 2 разрядов полученного слова, соответствующих контрольной сумме и самой этой контрольной суммы. Если , то считается, что передача прошла без ошибок. В случае одинарной ошибки будет равно двоичному числу-номеру сбойного бита. В случае ошибки, кратности большей 1, когда , ее можно обнаружить. Подобная схема декодирования не позволяет исправлять некоторые двойные ошибки, чего можно было бы достичь, используя схему декодирования с лидерами, но последняя значительно сложнее в реализации и дает незначительное улучшение качества кода.

Пример построения кодового слова квазисовершенного -кода, исправляющего все однократные ошибки, для сообщения 100011010.

Искомое кодовое слово имеет вид . Далее нужно вычислить контрольные суммы.

Таким образом, искомый код - 0011000111010. Если в процессе передачи этого кода будет испорчен его пятый бит, то приемник получит код 0011100111010. Для его декодирования опять вычисляются контрольные суммы:

Приемник преобразует изменением пятого бита полученное сообщение в отправленное передатчиком, из которого затем отбрасыванием контрольных разрядов восстанавливает исходное сообщение.

Совершенный код Хэмминга также можно строить по рассмотренной схеме, т.к. для него .

Для исправление одинарной ошибки к 8-разрядному коду достаточно приписать 4 разряда ( ), к 16-разрядному - 5, к 32-разрядному - 6, к 64-разрядному - 7.

Упражнение 41 Может ли -код, минимальное расстояние между кодовыми словами которого 5, быть совершенным?

Упражнение 42 Построить кодовые слова квазисовершенного -кода, исправляющего однократные ошибки, для тех сообщений, которые соответствуют числам 55, 200 и декодировать слова 1000001000001, 1100010111100, полученные по каналу связи, использующему этот код.