Главная | Обратная связь

Цель лабораторного занятия

 

Исследование 2-х уравнений методом «золотого сечения» и «простой итерации» с использования программного пакета Maple.

 

Задание на работу

1. Исследовать первое уравнение методом «золотого сечения» с помощью программного пакета Maple, вывести график.

2.Исследовать второе уравнение методом «золотого сечения» с помощью программного пакета Maple, вывести график.

 

Описание метода:

«Золотым сечением» называется деление отрезка в следующей пропорции:

Длина l исходного отрезка относится к длине l₁ большего отрезка так же, как длина последнего относится к длине l – l₁ меньшего под отрезка (рис. 1).

 

l₁ l – l₁

l

рис. 1

Математически это утверждение выражается следующим соотношением:

, которое может быть записано в виде квадратного уравнения:

x₁² + x₁ – 1 = 0.

Здесь x₁ = l₁/l. Решив это уравнение, получим .

Число g, определяемое выражением, называется «золотым сечением». Оно представляет собой предел при k → ∞ отношения числе Фибоначчи F_{k – 1} и F_k :

Алгоритм метода «золотого сечения» такой же, что и в методе Фибоначчи. Разница лишь в том, что построение подинтервалов унимодальности [x_{j – 1}, x_j] происходит путем их последовательного деления в отношении «золотого сечения» g:

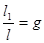
Таким образом, формулы примут вид:

x₁ = b – l₁ = b – lg,

x₂ = a + l₁ = a + lg.

 

По скорости сходимости метод «золотого сечения» уступает методу Фибоначчи. В то же время в некоторых случаях первый метод может оказаться более удобным, т.к. здесь деление отрезка всегда происходит в отношении постоянного числа g.

Выполнение работы

1. На основании алгоритма, описанного выше, составим структурную блок-схему «золотого сечения»:

 

Блок-схема метода «простых итераций»

 

 

 

2. Запишем программу в Maple, подставив значения своего варианта (см. Приложение №1).

3. Результат (промежуточный и конечный): корни и число итераций.

 

4.Отчет о проделанной работе должен содержать:

· Задание на работу

· Ход выполнения работы

· Полученные результаты работы.

· Выводы о проделанной работе

· Сравнительный анализ методов дихотомии и «золотого сечения» в табличной форме:

Методы	Уравнение 1	Уравнение 2
X	Y	N	X	Y	N
Метод дихотомии
Метод «золотого сечения»
Метод «простой итерации»

 

 

Лабораторная работа №3

"Метод Зейделя-Гаусса"